Äußere Einflüsse stören dynamische Stabilität von Wellenkupplungen

Anbieter zum Thema

b+s group

G+K Umformtechnik GmbH

AGTOS Gesellschaft für technische Oberflächensysteme mbH GmbH

FH Südwestfalen

Nicht unerwähnt sei der Einfluss, den die Vorverformung f0 und der betriebsbedingte Wellenversatz auf die Biegeeigenfrequenz ω des druckbelasteten Ringscheibenabschnitts haben; Bild 3 zeigt die Ergebnisse für den beidseitig gelenkig gelagerten beziehungsweise beidseitig eingespannten Druckstab mit axialer Auflagerverschiebung Δ.

Biegeeigenfreuquenzverhältnis steigt mit der Vorverformung des Druckstabs

Bei einem vorverformten Druckstab steigt mit der Vorverformung f0 das Biegeeigenfrequenzverhältnis ω/ω0 für bezogene Werte der Vorverformung

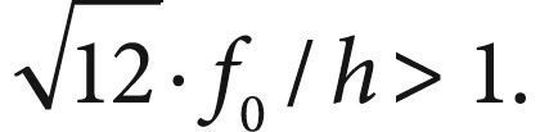
Nur für kleine Verhältnisse, das heißt

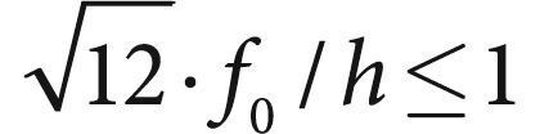
erhält man im Bereich kleiner Druckkräfte F – einhergehend mit geringen Auflagerverschiebungen – einen Bereich von Biegeeigenfrequenzverhältnissen ω/ω0 ≤1. Je weicher die Einspannstelle, um so stärker weicht die Biegeeigenfrequenz des Stabes mit Normalkraft von der des Stabes ohne Normalkraft ω0 ab.

Torsionsschwingungen vor allem von Wechselwirkung verschiedener Kräfte verursacht

Die Wechselwirkung von Gaskräften, Kolben, Pleuel und Kurbelwelle im Hubkolbenmotor ist die wichtigste Ursache von Torsionsschwingungen in Abtriebssträngen. Im Stabmodell der Ringscheibe entstehen Druckkräfte F(t) mit konstanter Last F0 und vereinfacht harmonischer Last F1 mit der Kreisfrequenz Ω zu

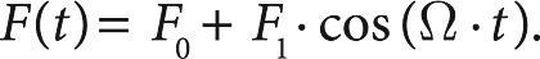
Die Kreisfrequenz Ω ist dabei im allgemeinen wesentlich geringer als die kleinste Eigenfrequenz der Stab-Längsschwingung. Der Stab erfährt dann infolge dieser Axiallast Biegeschwingungen; die Anregung in Querrichtung geschieht dadurch, dass die Axialkraft mit der doppelten Eigenfrequenz des Stabes pulsieren muss, so dass dieser jeweils bei Vorwärtsbewegung gedrückt und in der Rückwärtsbewegung gezogen wird.

Bild 4 und die Tabelle zeigen für verschiedene Lagerungsfälle den technisch interessanten Instabilitätsbereich. Vereinfacht kommt man zu vergleichbaren Ergebnissen für die kritische Längsschwingung Ωkrit, wenn man einmal mit der Belastung

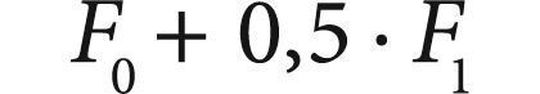
und einmal mit der Belastung

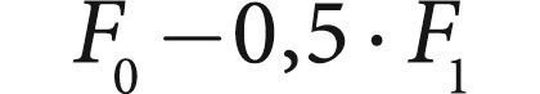
jeweils die unterste Biegeeigenfrequenz ermittelt und diese verdoppelt.

Literatur:

[1] Sturmath, R.: Federsteifen von Ganzstahl-Wellenkupplungen mit geometrisch unterschiedlichen Übertragungselementen, Antriebstechnik 25 (1986), Nr. 9, S. 65-68.

[2] Sturmath, R.: Massive Federlaschen und Ringpakete haben unterschiedliche Eigenschaften in Ganzstahl-Wellenkupplungen, MM Maschinenmarkt, Ausgabe 29, 1988, S. 48-52.

[3] Sturmath, R.: Ermittlung der Torsionssteifigkeit von Ringscheibenkupplungen, MM Maschinenmarkt, Ausgabe 5, 2005, S. 44-45.

[4] Weiss, H.: Erfahrungen mit flexiblen Ganz-stahl-, Laschen- und Ringkupplungen, VDI-Berichte 649, 1987, S. 119-136, VDI-Verlag.

[5] Akademischer Verein Hütte e.V.: Theoretische Grundlagen, 28. Auflage, 1955, Berlin.

Prof. Dr.-Ing. Rainer Sturmath lehrte Konstruktion an der Fachhochschule Südwestfalen in 59872 Meschede

(ID:347172)